Глава 3. Спектральные характеристики годичных ритмов личностных и психодинамических свойств

Как уже отмечалось в гл.1, архитектоника психоритмов --- их спектры, периодика, фазы, когерентность, стабильность --- являются уникальной характеристикой, ``психологическим портретом'' индивида, определяющим его адаптивный потенциал (И.П.Емельянов, 1976; Н.И.Моисеева, 1978; В.П.Казначеев, 1980; В.И.Шапошникова, 1991; И.Ю.Борисова, И.Е.Ганслина, Н.Я.Притыкина, 1996; А.А.Путилов, 1997). Однако в дифференциальной психологии и психофизиологии эвристические возможности биоритмологии до настоящего времени в должной мере недооценены. В данной работе ставилась цель --- изучить окологодичные (сезонные) ритмы в многоуровневой системе психофизиологической свойств индивидуальности.

В соответствии с представлениями об иерархической организации индивидуальности (U.Bronfenbrenner, 1951; В.С.Мерлин, В.В.Белоус, Б.А.Вяткин, Э.И.Маствилискер, 1973; В.М.Русалов, 1980; Э.А.Голубева, 1980; Г.А.Аминев, 1988; Б.А.Вяткин, 1993; М.Р.Щукин, 1994; Е.Д.Хомская, 1996; С.А.Изюмова, 1996; и др.). Мы провели последовательное экспериментальное изучение годичных ритмов свойств личностного, психодинамического, нейродинамического, микроэлементного и генетического уровней. Данные для первых двух уровней изложим в третьей, для нейро- и биодинамических уровней --- в четвертой главе.

3.1. Косинор-анализ личностных свойств

Методика исследования

В качестве испытуемых выступали студенты первого курса БашГУ в количестве 84 чел., возраст 17--18 лет, и выпускники Первой уфимской политологической гимназии --- 48 чел., возраст 16--17 лет. Личностные свойства определялись в режиме диалога компьютера с испытуемым, и использовали три теста: 16-ти факторный личностный опросник Кэттелла, форма ``С'' (R.B.Cattell, C.F.Stice, 1957; R.B.Cattell, H.W.Eber, 1970); опросник Леонгарда-Шмишека --- четыре личностные шкалы (К.Леонгард, 1981; Г.А.Аминев, Э.Г.Аминев, 1994), тест Фрейда на определение нейротипов (S.Freud, 1953; Г.А.Аминев, Э.Г.Аминев, 1994).

Испытуемые разбивались на 12 подгрупп в соответствии с датой их рождения по зодиаку, рассчитывались средние и стандартные отклонения. В итоге получили 26 помесячных динамик показателей: 17 --- по тесту Кэттелла, 4 --- Леонгарда-Шмишека, 5 --- по тесту Фрейда.

Для каждой динамики проводился периодограммный и косинор- анализы, рассчитывали период, фазу, амплитуду, мезор, как описано в гл.2. Обращаем внимание, что амплитуда колебаний зависит от того, в каких единицах измеряется тот или иной показатель, от количества вопросов в шкалах. Для элиминации этого фактора все тесты приводились к одной масштабной шкале, а именно сырые баллы переводились в Т-баллы. Это позволяло строить косиноровы эллипсы для разных тестов на одном графике и сопоставлять их.

3.1.1. Иллюстрирующий пример

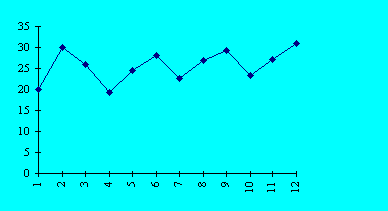
Для демонстрации годичных ритмов остановимся на одном примере. Для этого взяли важное для социальной практики качество --- способность к самоконтролю, определяемую по шкале ``Сила торможения'' теста Я.Стреляу. В табл. 3.1 представлена динамика средних значений за каждый месяц (второй столбец). Как видим, это колеблющийся ряд, и сырые баллы лежат в пределах от 19.4 до 30.9 единиц. В Т-баллах имеем преобразованный ряд, который располагается в коридоре нормы и приходится на диапазон от 40.68 до 58.21.

Для наглядности эти данные изображены на рис. 3.1.

Из рисунка видим, что колебания силы торможения не случайные, а представляют серию волн длиной периода Т = 3 мес. Начиная с января сила торможения увеличивается, затем с февраля снижается, к апрелю достигает минимума, и далее весь процесс повторяется. В конце года периодичность не нарушается, ибо после декабря к январю следующего года происходит спад, и период оказывается равным трем месяцам.

Примечание. По оси ОХ --- месяц рождения, по оси ОУ --- средние значения шкалы ``Сила торможения'' за соответствующий месяц.

Возникает вопрос, являются ли эти колебания силы торможения случайными, или же они подчинены определенному ритму. Для ответа на него мы проводили два вида математико-статистической обработки: метод корреляционных периодограмм и косинор-анализ.

А. Метод корреляционных периодограмм

Суть метода корреляционных периодограмм сводится к тому, что экспериментальная кривая сопоставляется с серией пробных косинусоид с различными периодами и начальными фазами. Для ясности они представлены в следующих столбцах табл. 3.1.

Сначала компьютер ищет, нет ли периодичности годичной. Для этого экспериментальная кривая сопоставляется с 12-месячными косинусоидами, имеющими различные фазы от 0 до 11 месяцев. Сопоставление производится путем рассчета коэффициентов корреляции (В.Ю.Урбах, 1963; Г.В.Суходольский, 1976; Г.А.Аминев, 1982).

Таблица 3.1. Динамика средних значений силы торможения по тесту Я.Стреляу

Примечание: СБ --- средние сырые баллы за месяц, ТБ --- помесячные Т-баллы, cos X-Y означает косинусоиду с периодом X и акрофазой Y месяцев, r --- коэффициент корреляции, умноженный на 100. Средний сырой и стандартное отклонение балл по контингенту 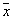=25.5, s = 6.5, N = 67. Уровни значимости r₀₅=0.576, r₀₁=0.708.

Из последней строки видим, что корреляции r пробных косинусоид с периодом в один год с динамикой силы торможения менялись в пределах от -0.27 до +0.27, но ни одна из них не достигла критического уровня значимости (P>0.05), в том числе и косинусоида с фазой 10 месяцев, которая дала максимальное соответствие с экспериментом (r = 0.27).

Но это еще не означает, что, вообще, во временном тренде силы торможения нет ритмичности, так как колебания могут происходить с частотой гармоник и иметь периоды в 6, 4, 3, 2 месяца. И, наконец, даже суточные ритмы не равны точно 24 часам (Ю.Ашофф, 1984). Поэтому реальные периодичности могут быть окологодичными и иметь отличные значения от вышеозначенных. С учетом сказанного компьютерный поиск ритмических составляющих производился для всех остальных периодов, начиная с периода 11 и завершая 2 месяцами. При этом компьютер для каждого очередного пробного периода перебирал всевозможные фазы и определял косинусоиду, максимально по абсолютному значению коррелирующую с экспериментом.

Результаты этих расчетов сведены в таблицу 3.2, из которой хорошо видно, что некоторые косинусоиды совершенно не синхронны с экспериментальной кривой (корреляции малозначимы).

Таблица 3.2. Корреляционная периодограмма годичной динамики силы торможения по тесту Я.Стреляу

Примечание: коэффициенты корреляции умножены на 100, N = 67, r₀₅=0.576, r₀₁=0.708.

Если рассматривать абсолютные значения коэффициентов корреляции, то наилучшим приближением является cos3-1, которая находится в противофазе к экспериментальной кривой (r = -0.85, P<0.01). Следовательно, экспериментальная кривая описывается гармонической моделью с периодом Т = 3 мес и начальной фазой Т₀ = 2.5 мес.

Для наглядности эти материалы изображены на рис. 3.2.

Б. Косинор-анализ

Периодограммный анализ дает значение периода, а для точного определения фазы требуется постепенное приближение путем ее дробления. Более быстрое решение дает косинор-анализ, который позволяет определить ``полный набор'' других, помимо периода, характеристик ритма: акрофазу, амплитуду и мезор (Ю.В.Линник, 1962; К.А.Багриновский, Н.В.Багинская, А.Ф.Баженова, 1973; И.П.Емельянов, 1976, 1986; W.Nelson, Y.L.Tong, J.K.Lee, F.Halberg, 1979). Аппарат аппроксимации косинусоидой подробно описан во второй главе. После выполнения этой процедуры в нашем примере получаем интересующие нас показатели колебательного процесса:

акрофаза j = 2.59 мес,

амплитуда А = 4.40 сырых балла,

мезор h = 25.71 сырых балла,

соотношение амплитуды и стандартного отклонения m = 0.68,

соотношение сигнал/шум К = 2.91.

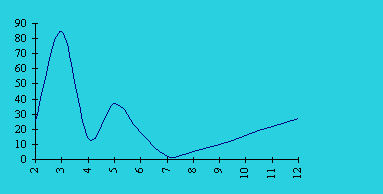
Итак, сила торможения колеблется с периодом 3 месяца, начальной фазой 2 мес 18 дней. Средний уровень флуктуаций (мезор) составляет 25.7 балла, амплитуда --- 4.4 балла. Следовательно, колебания происходят в коридоре от 21.3 до 30.1 балла. Так как величина силы торможения измерялась в сырых баллах, то для характеристики интенсивности колебаний вводится параметр, равный соотношению амплитуды колебаний и стандартного отклонения: m = А/s. В нашем случае амплитуда колебаний составляет две третих от величины разброса замеряемого психофизиологического показателя (или 68%). Интенсивность влияния геофизических факторов на колебания силы торможения выражает также отношение сигнала к шуму, из которого явствует, что величина полезного сигнала почти в три раза превышает уровень шума, т.е. колебаний вызванных случайными факторами.

Наглядно эти данные представлены на рис. 3.3, и мы можем убедиться в регулярности флуктуаций силы торможения.

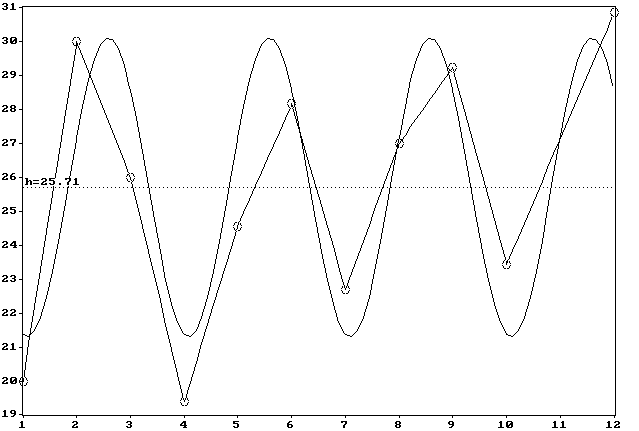
Оценка статистической значимости сходства психоритма с косинусоидой производится методом сравнения дисперсии самого изучаемого процесса Dэкс и дисперсии его отклонения от модельной косинусоиды Dразн с помощью критерия Фишера (В.Ю.Урбах, 1963):

Dэкс = 14.13, Dразн = 3.55,

F₀₁ = 3.98, F₀₅ = 2.69, P < 0.05.

Критерий Фишера получился больше критического значения, и, следовательно, экспериментальная кривая, в данном случае годичная динамика силы торможения, действительно, аппроксимируется косинусоидой с периодом Т=3 мес и фазой j = 2.59 мес с достоверностью P < 0.05. Это согласуется с корреляционным критерием периодограммного анализа: r = 0.85 , P < 0.01. Точность процедур поиска подтверждается также совпадением акрофаз, найденных различными способами: в первом случае экспериментальная кривая аппроксимировалась косинусоидой с периодом и акрофазой, соответственно равным 3 и 2.5 месяцам, во втором случае --- с тем же периодом и акрофазой, равной 2.59.

В силу этого в дальнейшем для каждого свойства индивидуальности приводятся следующие показатели: среднее значение и стандартное отклонение по контингенту, период, акрофаза (начальная фаза), амплитуда колебаний, мезор (средний уровень колебаний), отношение амплитуды колебаний к стандартному отклонению, отношение полезного сигнала к шуму, коэффициент корреляции экспериментальной кривой и теоретической косинусоиды.

3.1.2. Косинор-анализ личностных свойств

Подобная обработка производилась со всеми замеренными нами разноуровневыми свойствами индивидуальности, и после иллюстрирующего примера можем перейти к систематическому рассмотрению полученных материалов. Экспериментальные для годичных колебаний свойств личностного уровня приводятся в табл. 3.5.

Таблица 3.5. Годичная динамика личностных свойств

Примечание: шкалы теста Кэттелла: A --- общительность, B --- сообразительность, C --- эмоциональная устойчивость, E --- независимость, F --- беспечность, G --- сила "Я", H --- смелость, I --- мягкость, L --- подозрительность, M --- непрактичность, N --- прямолинейность, O --- тревожность, Q1 --- склонность к новаторству, Q2 --- самостоятельность, Q3 --- высокий самоконтроль, Q4 --- напряженность, MD --- лживость; шкалы теста Леонгарда-Шмишека: Де --- демонстративность, Пе --- педантичность, За --- застреваемость, Во- возбудимость; шкалы теста Фрейда: О --- оральный тип, А --- анальный тип, У --- уретральный тип, Ф --- фаллический тип, Г --- генитальный тип.

Обозревая, замечаем, что все показатели от месяца к месяцу флуктуируют, и неясно, имеется ли при этом определенная ритмика. Результаты периодограммного и косинор-анализа, проясняющие этот вопрос, представлены в табл. 3.6.

Таблица 3.6. Результаты периодограммного и косинор- анализов годичной динамики личностных свойств

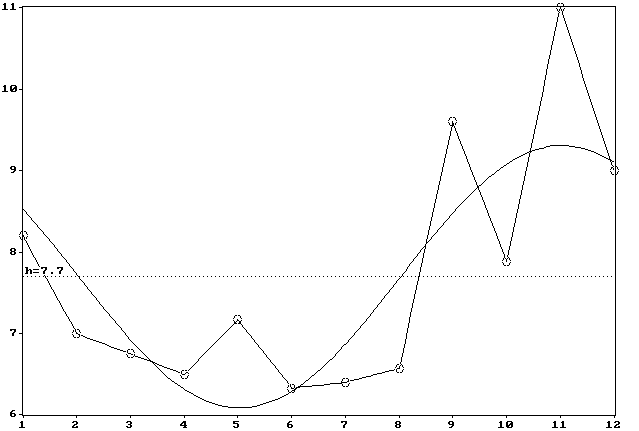
Примечание: 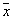--- среднее значение сырых баллов; s --- стандартное отклонение; Т --- период; j --- акрофаза; А --- амплитуда колебаний в сырых баллах; h --- мезор, или средний уровень колебаний; m --- отношение А к s; К --- отношение полезного сигнала к шуму; r --- коэффициент корреляции экспериментальной и теоретической косинусоиды. Коэффициенты корреляции умножены на 100, r₀₅ = 0.576, r₀₁ = 0.708, N = 74.

В третьем и четвертом столбцах таблицы приводятся средние значения и стандартные отклонения сырых баллов по контингенту в целом. В последующих столбцах сведены характеристики аппроксимирующих косинусоид. Начнем их рассмотрение прежде всего с вопроса статистической значимости.

Из последнего столбца хорошо видно, что максимальные значения корреляций косинусоид с экспериментальными данными колеблются от 0.47 (P > 0.05) до 0.80 (P < 0.01) и для 17 свойств достигают уровня значимости P<0.05. Для прояснения смысла этого результата напомним, что при периодограммном анализе ритмичность верифицировалась расчетом коэффициентов корреляций r между исходной кривой и 77-ю гармоническими моделями годичных ритмов (12 + 11 + 10 + ... + 2 = 77 проб). На языке теории вероятностей это равнозначно тому, что каждому свойству предоставлялся шанс из 77 выборов быть коррелированным с каким-либо ритмом, и из 26 свойств этим шансом ``воспользовались'' 17.

Этот результат однозначно свидетельствует о том, что годичная периодичность является закономерным явлением и отражает влияние геофизических факторов на свойства личностного уровня. При этом вовлеченность личностных качеств в этот процесс составляет n = 17/26 = 65%.

Напомним, что коэффициенты корреляции, из которых он получен, не определяют направления связи, так как если Х коррелирует с У, то нельзя сказать, что из них является первичным и что вторичным. В случае с годичными биологическими ритмами ситуация проще (ведь никто же не станет утверждать, что линька зайцев определяет смену времен года). Поэтому степень вовлеченности n в годичные ритмы, очевидно, зависит от мощности влияния ритмоформирующих геофизических факторов на личностные качества, а не наоборот. Учитывая эти соображения, назовем далее показатель n экстенсивной мерой геофизических влияний на индивидуальность, в данном разделе на уровень личностных свойств. Экстенсивной эта характеристика названа по той причине, что показывает диапазон охвата личностных свойств управляющими воздействиями геофизического фактора.

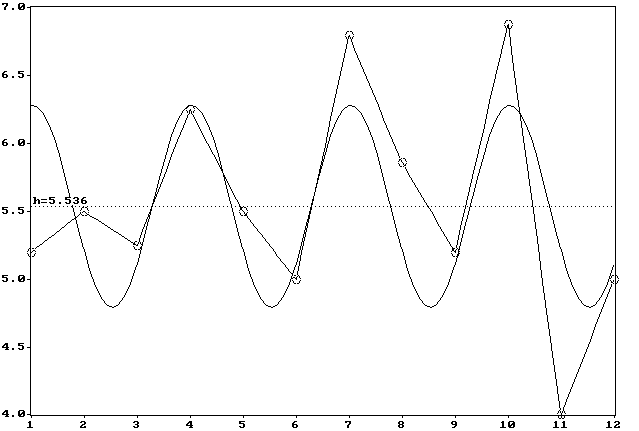
Сила влияния геофизических ритмоводителей проявляется в отношении полезного сигнала к шуму в кривых годичной динамики, и этот параметр менялся в пределах от 0.30 до 2.31. Это показывает, что в ряде случаев гармоническая составляющая колебаний личностных свойств более, чем в полтора--два раза, превышает уровень случайного фактора (шума). Это хорошо видно на рис. 3.4 (a, b), на котором изображены годичные колебания подозрительности L (период 3 мес, фаза 1 мес, r = 0.68, P < 0.05) и склонности к риску Н (период 12 мес, фаза 11 мес, r = 0.80, P < 0.01), соответствующие наиболее типичным, как это будет показано далее, периодичностям.

Примечание. По оси ОХ --- месяц рождения, по оси ОУ --- средние значения шкалы ``Подозрительность'' за соответствующий месяц. r₀₅ = 0.68.

Примечание. По оси ОХ --- месяц рождения, по оси ОУ --- средние значения шкалы ``Склонность к риску'' за соответствующий месяц. r₀₁ = 0.80.

Еще более отчетливее геофизические факторы отражаются на амплитуде колебаний. В нашем случае амплитуда зависит от интервала разброса сырых баллов. Поэтому напрямую сравнение различных свойств невозможно, так как необходимо привести их к единой мере, что мы и сделали путем деления амплитуды на стандартное отклонение. Полученные числа можем назвать интенсивной мерой влияния геофизических факторов: m = А/s. Как видно из таблицы, m лежал в диапазоне от 0.45 до 1.48, т.е. амплитуда сезонных колебаний отдельных свойств составляла от половины до полутора значений стандартных отклонений.

Остается изучить функцию распределения свойств личности по длине периода годичных ритмов и их гармоник (рис. 3.5):

Примечание: по оси ОХ --- величина периода, по оси OY --- его частота в %.

Видим, что функция распределения имеет хорошо выраженный пик в полосе быстрых трехмесячных ритмов и некоторый подъем в окологодичном диапазоне (11--12 месяцев). Следовательно, личностные свойства индивидуальности регулируются двумя ритмическими составляющими геофизического фактора. Если годичные ритмы рассматривать как вектор регуляций, то выделение двух компонентов означает, что регуляция личностных свойств подчиняется принципу кодирования номером канала Е.Н.Соколова (см. Ч.А.Измайлов, Е.Н.Соколов, 1978; Е.Н.Соколов, 1995; Н.Н.Данилова, А.Л.Крылова,1997; подробнее см. Заключение).

Возникает вопрос, как соотносятся между собой описанные выше показатели ритмики? Для этого воспользовались корреляционно-факторным анализом (табл. 3.7 и табл. 3.8).

Таблица 3.7. Корреляционная матрица характеристик колебаний годичной динамики личностных свойств

Примечание: жирным шрифтом выделены достоверные корреляции, N = 23, Р₀₅  = 0.413, Р₀₁  = 0.526.

Таблица 3.8. Факторная структура характеристик колебаний годичной динамики личностных свойств

Примечание: СЗ --- собственные значения, НОСЗ --- накопленные отношения собственных значений, N = 23, F₀₅ = 0.41, F₀₁ = 0.53.

Специфичными для первого фактора стали мезор (0.942), среднее значение (0.936) и стандартное отклонение (0.919), у которых значимые веса, и они не вошли ни в какие другие факторы. Изложенное изобразим условной формулой F1 = (h + 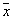 + s), и назовем этот фактор фактором среднего значения сырого балла. При дальнейшем анализе он не используется, так как зависит от технических характеристик теста.

Во второй фактор F2 = (К + r + m ) вошли отношение полезного сигнала к шуму (0.877), коэффициент корреляции экспериментальной кривой с теоретической косинусоидой (0.849) и отношение амплитуды колебаний к стандартному отклонению (0.785). Это фактор интенсивности связей колебаний личностных свойств и геофизических ритмоводителей. Из строки накопленных значений следует, что изменчивость личностных свойств в целом объясняется степенью воздействия геофизических факторов на 64.7 - 35.7 = 29%.

Для третьего фактора F3 = (T + j ) специфичными стали период (0.862) и акрофаза (0.857). Это фактор периодичности колебаний личностных свойств.

Если к этим трем факторам добавим экстенсивную меру геофизических влияний на индивидуальность, то имеем три (без учета F1) системные характеристики взаимодействия колебаний личностных свойств и геофизических факторов.

3.2. Косинор-анализ темпераментальных свойств

Подобные гармонические колебания были обнаружены и для темперамента (в дифференциальной психофизиологии темперамент обозначают также термином психодинамика). Психодинамические свойства были изучены с помощью тестов Айзенка (Г.А.Аминев, 1977), Спилбергера-Ханина (Ю.Л.Ханин, 1976, 1980; Ч.Д.Спилбергер, 1983), Шварца (И.Е.Шварц, 1971) и шести шкал акцентуаций характера по Леонгарду-Шмишеку (К.Леонгард, 1981; Г.А.Аминев, Э.Г.Аминев, 1994). Экспериментальные данные для годичной динамики свойств темпераментального уровня приведены в табл. 3.9.

Таблица 3.9. Годичная динамика темпераментальных свойств

Примечание: шкалы теста Айзенка: Э --- экстроверсия, Н --- нейротизм, Л --- лживость; шкалы теста Спилбергера-Ханина: СТ --- ситуативная тревожность, ЛТ --- личностная тревожность; шкала теста Шварца: ВН --- внушаемость; шкалы теста Леонгарда-Шмишека: ГИ --- гипертимность, ДИ --- дистимность, ЦИ --- циклотимноть, ЭК --- экзальтированность, ЭМ --- эмотивность, ТР --- тревожность.

При просмотре по месяцам вновь нетрудно заметить флуктуацию показателей. Периодограммный и косинор- анализ (табл. 3.10) выявили наличие четкой, статистически значимой периодичности. Коэффициенты корреляции r между экспериментальными и теоретическими данными, как это ясно из последнего столбца, колеблются от 0.46 (P > 0.05) до 0.83 (P < 0.01). На 12 свойств психодинамического уровня статистически достоверных коэффициентов корреляции (P<0.05) оказалось 9, т.е. коэффициент управляемости психодинамического уровня индивидуальности геофизическими факторами составляет n = 75%.

Таблица 3.10. Результаты периодограммного и косинор- анализов годичной динамики психодинамических свойств

Примечание: 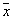--- среднее значение сырых баллов; s --- стандартное отклонение; Т --- период; j --- акрофаза; А --- амплитуда колебаний в сырых баллах; h --- мезор, или средний уровень колебаний; m --- отношение А к s; К --- отношение полезного сигнала к шуму; r --- коэффициент корреляции экспериментальной и теоретической косинусоиды. Коэффициенты корреляции умножены на 100, r₀₅=0.576, r₀₁=0.708, N = 69.

Из таблицы 3.10 также видим, что соотношение сигнала к шуму (К) в кривых годичной динамики темперамента меняется в пределах от 0.29 до 2.82. Следовательно, в ряде случаев гармоническая составляющая колебаний психодинамических свойств почти в три раза превышает уровень случайного фактора (шума), например, таковым свойством является внушаемость по Шварцу (рис. 3.6). Показатель интенсивной меры влияния геофизических факторов (m) лежал в диапазоне от 0.61 до 1.18.

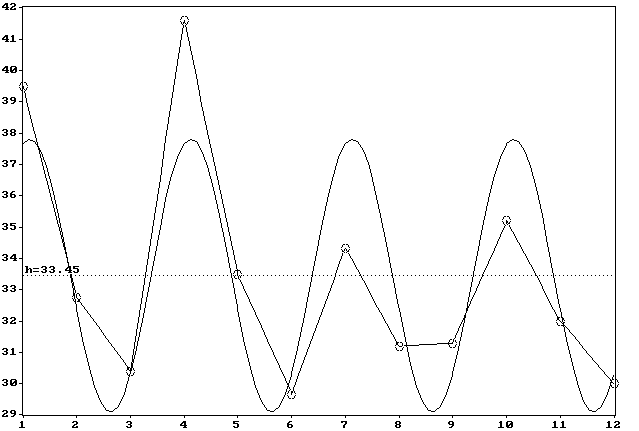
Примечание. По оси ОХ --- месяц рождения, по оси ОУ --- средние значения за соответствующий месяц. r₀₁ = 0.83.

Далее изучим кривую распределения частоты периодов ритмов психодинамического уровня (Рис. 3.7).

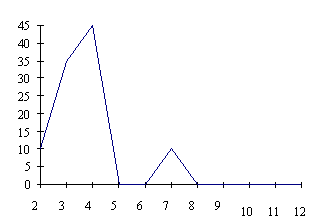
Видим, что функция распределения свидетельствует о наличии четко выраженного узкополосного спектра в диапазоне быстрых четырех-трехмесячных ритмов. Следовательно, темпераментальные свойства индивидуальности регулируются быстрыми ритмами.

Проанализируем взаимосвязь показателей ритмики психодинамических свойств, используя аппарат корреляционно-факторных расчетов (табл. 3.11 и табл. 3.12).

Таблица 3.11. Корреляционная матрица характеристик колебаний годичной динамики темпераментальных свойств

Примечание: жирным шрифтом выделены достоверные корреляции. N = 11, Р₀₅ = 0.6, Р₀₁ = 0.74.

Из таблицы 3.12 видим, что специфичными для первого фактора F1 = (s +  А + h + 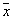), стали стандартное отклонение (0.966), амплитуда (0.908), мезор (0.899) и среднее значение (0.899).

Во второй фактор F2 = (r + m + К) интенсивности связей колебаний личностных свойств и геофизических ритмоводителей вошли коэффициент корреляции экспериментальной кривой с теоретической косинусоидой (-0.926) и отношение амплитуды колебаний к стандартному отклонению (-0.899), отношение полезного сигнала к шуму (-0.858). Из последней строки следует, что изменчивость психодинамических свойств в целом объясняется воздействием геофизических факторов на 82.2 - 65.7 = 16.5%.

Таблица 3.12. Факторная структура характеристик колебаний годичной динамики темпераментальных свойств

Примечание: СЗ --- собственные значения, НОСЗ --- накопленные отношения собственных значений, N = 11, F₀₅ = 0.602, F₀₁ = 0.735.

Для третьего фактора F3 = (j + T) (фактор периодичности колебаний темпераментальных свойств) специфичными стали акрофаза (0.793) и период (0.680). Таким образом, факторная структура характеристик геофизических годичных ритмов, управляющих личностными и психодинамическими свойствами совпадает: в обоих случаях выделяются три фактора (один --- экстенсивный, второй --- интенсивный и третий --- периодичности). Но по архитектонике геофизических годичных ритмов эти уровни индивидуальности различались, так как личностные свойства подчиняются трехмесячным и окологодичным ритмам, а темпераментальные --- четырех-трехмесячным ритмам.

3.3. Косиноровы эллипсы для личностных и психодинамических ритмов

Если свойства индивидуальности объединились в классы одинаковой периодичности, это еще не означает их психоритмологическую эквивалентность, ибо ритмы одного периода могут отличаться фазами. Изучение фазовых соотношений производится в косинор-анализе построением эллипсов равных вероятностей (И.П.Емельянов, 1976, 1986). Напомним, как строится эллипс. Каждый ритм рассматривается как вектор с двумя полярными координатами --- амплитудой колебаний и акрофазой --- и представляется на координатной плоскости в виде точки. Так как амплитуда зависит от характеристик теста, то она должна быть нормирована, и мы пользуемся так называемыми Т-баллами, едиными для всех тестов. При этом условии, если точки различных свойств расположатся кучно, мы можем считать, что они образуют один ритмологический ансамбль. При этом по расположению точек внутри эллипса можно определить временные соотношения: какие свойства в течение года запускаются раньше, какие позже. Это и составляет фазовую архитектонику ритмов.

На рис. 3.8 изображен эллипс равных вероятностей для трехмесячных ритмов личностных свойств индивидуальности. Видим, что точки, репрезентирующие личностные ритмы, расположились в зоне 95-процентного двумерного эллипса распределения, расположенного выше начала координат. Это означает, что изучаемые личностные свойства образовали единый ансамбль, так как их фазы не распределились случайным образом на всей фазовой плоскости.

В силу этого можем говорить о достоверной (P < 0.05) последовательности ритмов, которая и характеризует временную архитектонику ритмов. Если двигаться против часовой стрелки, то можно выяснить, в какой очередности геофизические факторы индуцируют ритмику личностных качеств. Первыми включаются качества, характеризующие мягкость, доброту (шкала I Кэттелла) и щедрость к людям (шкала, обратная А-типу по Фрейду); на рисунке это шестая и пятая точки. Далее генерируются подозрительность, злопамятность --- шкала L Кэттелла и застреваемость по Леонгарду-Шмишеку (вторая и четвертая точки). И, наконец, последними в этом диапазоне следуют зависимость и стремление быть незаметными --- полярные значения шкал G Кэттелла и демонстративности по Леонгарду-Шмишеку (первая и третья точки).

Примечание: точки, изображенные на плоскости, соответствуют свойствам личностного уровня: 1 --- независимость (тест Кэттелла); 2 --- подозрительность (тест Кэттелла); 3 --- демонстративный тип (тест Леонгарда-Шмишека); 4 --- застревающий тип (тест Леонгарда-Шмишека); 5 --- анальный тип (тест Фрейда); 6 --- генитальный тип (тест Фрейда). Для подчеркнутых шкал брались полярные значения. j min = 0.31, j max = 1.51.

Физический смысл этих результатов проясняется, если учесть, что мы изучаем динамику свойств по месяцам рождения. В таком случае приведенные данные показывают, что трехмесячные ритмы образуют ансамбль, поочередно запускаемых процессов: сначала к концу первой декады трехмесячного цикла рождаются индивиды мягкие и доброжелательные, затем к концу первого месяца начинают рождаться подозрительные, мстительные, и конец первой декады второго месяца знаменуется рождением людей с низкой самооценкой.

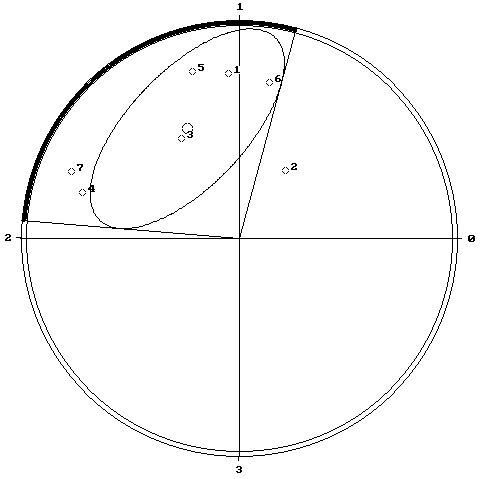
Примечание: точки, изображенные на плоскости, соответствуют свойствам темпераментального уровня: 1 --- экстраверсия (тест Айзенка); 2 --- внушаемость (тест Шварца); 3 --- дистимность (тест Леонгарда-Шмишека); 4 --- циклотимность (тест Леонгарда-Шмишека); 5 --- экзальтированный (тест Леонгарда-Шмишека); 6 --- тревожный (тест Леонгарда-Шмишека); 7 --- интроспективность (тест ``Индивидуальная анализируемость''). Для подчеркнутых шкал брались полярные значения. j min = 0.83, j&mbsp;max = 1.95.

Перейдем к рассмотрению эллипса равных вероятностей для четырехмесячных ритмов психодинамических свойств индивидуальности (см. рис. 3.9). Рассуждая аналогичным образом, получаем, что в середине первого месяца четырехмесячного цикла рождаются люди доверчивые и внушаемые, а в конце его --- тревожные. Далее в самом начале второго месяца появляются индивиды сдержанные, замкнутые, затем примерно через неделю ``природа уравновешивает'' их людьми экзальтированными, восторженными. Далее следуют люди восторженные (по Леонгарду-Шмишеку). В конце второго месяца рождаются люди открытые (по тесту ``Индивидуальная анализируемость'') и стабильные, эмоционально устойчивые (по Леонгарду-Шмишеку).

3.4. Выводы

Учитывая изложенное в данной главе, можем сделать следующие выводы:

1. Впервые в экспериментальной психологии проведено исследование годичных ритмов колебаний системы иерахических свойств индивидуальности. Показана возможность эффективного использования метода корреляционных периодограмм и косинор-анализа для статистически надежного выявления ритмических составляющих и расчета основных параметров: периода, акрофазы, мезора, амплитуды, соотношения амплитуды и стандартного отклонения, соотношения сигнал/шум.

2. Показано, что в колебаниях большинства свойств личностного уровня (n = 65%) имеется годичная периодичность, характеризуюшая меру экстенсивности геофизических влияний на личностные качества индивидуальности. Сила влияния геофизических ритмоводителей выражалась отношением полезного сигнала к шуму в кривых годичной динамики, которое от свойства к свойству менялось в пределах от 0.30 до 2.31, свидетельствуя о том, что гармоническая составляющая колебаний личностных свойств может более чем в полтора--два раза превышать уровень случайного фактора (шума).

   Распределение ритмов личностного уровня по длительности периодов имеет хорошо выраженный пик в полосе быстрых трехмесячных ритмов и некоторый подъем в окологодичном диапазоне (11--12 месяцев). Следовательно, регуляция личностных свойств так же, как и регуляция частоты сердечных сокращений, подчиняется принципу кодирования номером канала Е.Н.Соколова (1995) и осуществляется двумя ритмическими составляющими геофизического фактора.

   Корреляционно-факторный анализ показал, что личностные ритмы образуют единую систему, параметры которых группируются по трем факторам:

   • среднего значения сырого балла тестов;
   • интенсивности связей колебаний личностных свойств и геофизических ритмоводителей (в него вошли отношение полезного сигнала к шуму, коэффициент корреляции экспериментальной кривой с теоретической косинусоидой, отношение амплитуды колебаний к стандартному отклонению);
   • третий фактор --- периодичности колебаний личностных свойств (период и акрофаза).
   Если к этим трем факторам добавить экстенсивную меру геофизических влияний на индивидуальность, то имеем три (без учета F1) системные характеристики взаимодействия колебаний личностных свойств и геофизических факторов.

3. Аналогичная статистически значимая ритмичность обнаружена во флуктуациях показателей психодинамического (темпераментального) уровня, при этом степень охваченности исследованных свойств ритмами составила 75%, а отношение сигнала к шуму (К) находилось в пределах 0.29--2.82, т.е. по ряду свойств амплитуда ритмов почти в три раза превышала уровень шума.

   По функции распределения периодов установлено, что темпераментальные свойства индивидуальности отличаются от личностных, так как регулируются быстрыми ритмами в диапазоне трех-четырех месяцев. Факторная структура параметров ритмики для обоих уровней была идентичной.

4. Методом косиноровых эллипсов установлено, что годичные ритмы образуют ансамбль взаимосвязанных процессов не только по периодичности, но и по фазе, характеризующий то, в какой последовательности индуцируются элементы ритмического ансамбля геофизическими факторами.

   Трехмесячные личностные ритмы образуют фазовую структуру, в которой к концу первой декады трехмесячного цикла рождаются индивиды мягкие и доброжелательные, затем к концу первого месяца --- подозрительные, мстительные, и конец первой декады второго месяца знаменуется рождением людей с низкой самооценкой.

   Фазовая структура четырехмесячных ритмов психодинамики также характеризовала то, в какой последовательности запускаются в популяции процессы рождения индивидов с различными свойствами: к концу первого месяца рождаются люди доверчивые, внушаемые, тревожные; затем в самом начале второго месяца наступает время сдержанных, замкнутых, но уже через неделю ``природа уравновешивает'' их людьми экзальтированными, восторженными, открытыми.

Таким образом, в годичных флуктуациях большинства личностных и психодинамических свойств индивидуальности, связанных с временем рождения, имеется четкая периодичность, организованная в единую систему последовательно запускаемых процессов.

Оглавление